Regressing Dynamic System Parameters from Poincare Maps
Poincare maps can be used to analyze dynamical systems. They have an interesting property in that different dynamical system parameters (say, the mass of a pendulum) result in human-perceptable, surprisingly smoothly changing characteristics in the Poincare map, even if the underlying trajectories integrated to obtain the maps are highly chaotic. This is notable since estimating the parameters of a dynamical system from trajectory data has proven challenging for chaotic systems. We show that a ResNet can exploit the smoothly changing visual characteristics of Poincare maps to regress a dynamical system’s parameters, given a training dataset of Poincare maps for the same system with various parameters. We show that with basic data augmentation you can address some issues that emerge in applying this method in practice, such as the need to make predictions on data coming from trajectories integrated for different lengths of time, or with fewer sampled initial conditions.
| Figure 1: Real-time construction of Poincare maps for the Swinging Atwood's Machine (SAM) in a stable (red) and chaotic (green) configuration. On the left is the system configuration, on the right is the Poincare-Map representation of the system. |
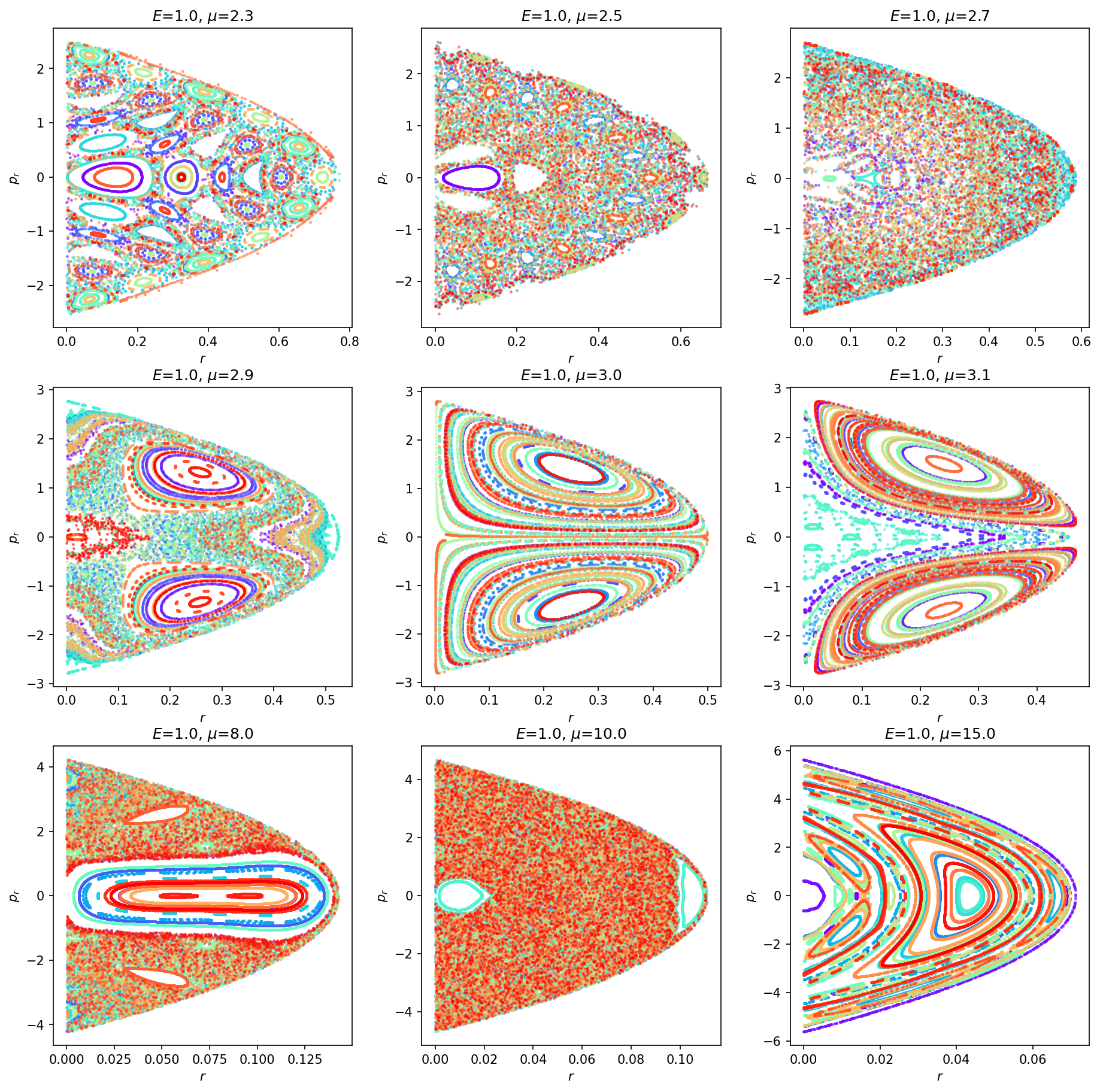
Figure 2: Sampled Poincare maps for the Swinging Atwood's Machine (colours correspond to trajectories from different initial configurations) for various values of the system's mass-ratio parameter, μ. |
|
|
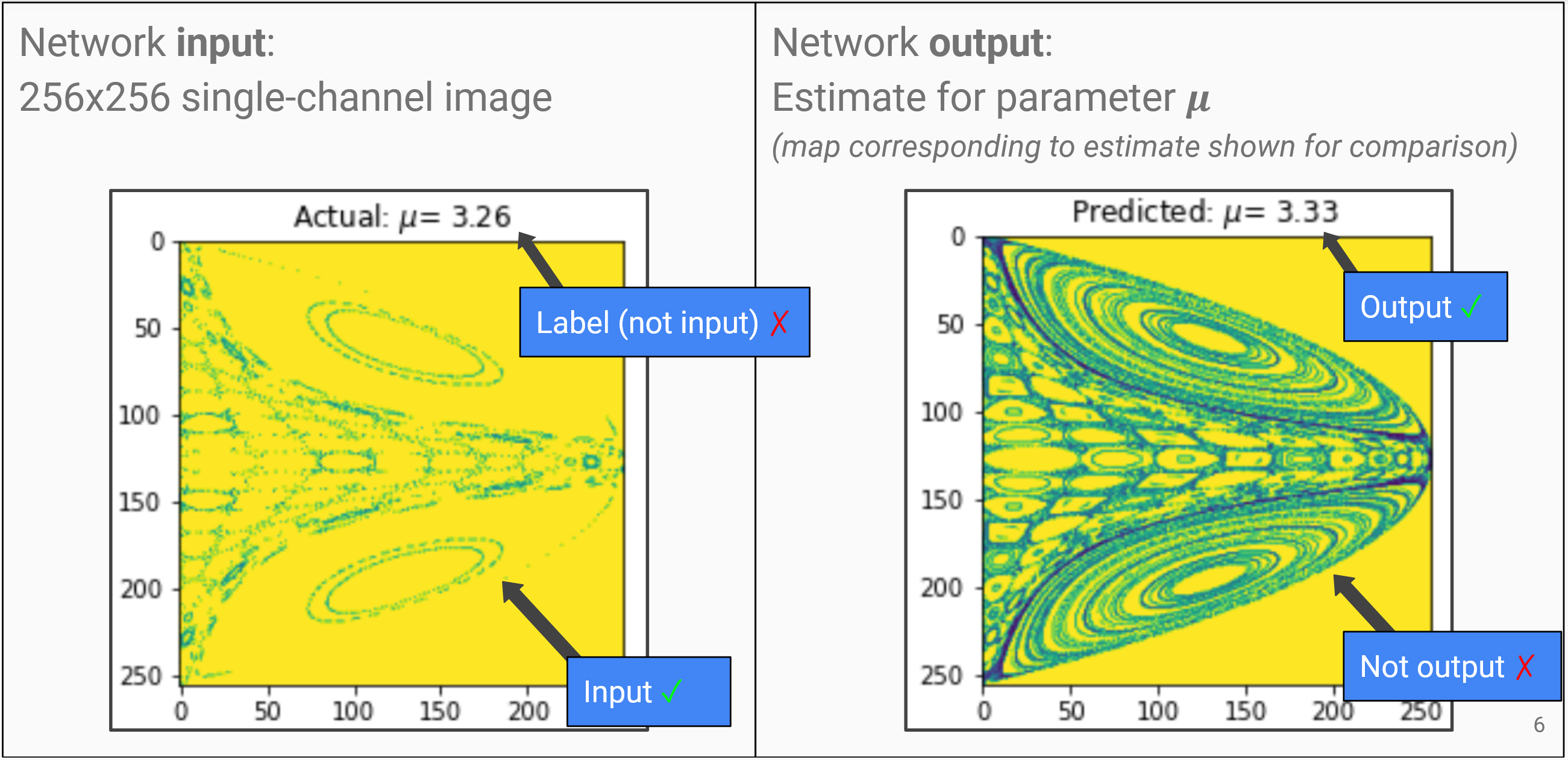
| Figure 3: An example input-output for a ResNet trained to estimate the mass ratio parameter of the SAM system which produced the Poincare map (left) input to the network. On the right is the parameter estimate, along with a higher quality (trajectories integrated from more initial conditions, for longer) Poincare map corresponding to the network's estimated parameter. |
|


